공간상에서 임의의 세 점이 주어지면, 구하고자 하는 각이 있는 점을 원점으로 하는 두 벡터를 구할 수 있습니다.



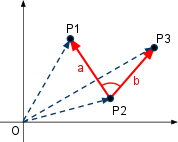
두 벡터가 주어졌을 때, 두 벡터의 사이각을 구하는 것은 보통 내적을 이용합니다.



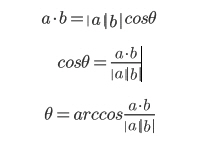
내적을 성분으로 구하는 것은 알고 있겠지요.... ㅡ.ㅡㅋ...

내적의 경우 0~180의 값만을 알 수 있습니다. (삼각형의 내각은 최대 180도라고 하는 것과 같습니다.) 180도 이후의 값은 180도 이내의 값과 구별이 안됩니다. 따라서 추가로 정보가 필요합니다.

0~360의 각을 알고자 할 때는 두 벡터 사이의 위치 관계를 알아야 하는데, 이것은 외적을 이용하면 알 수 있습니다.
(각이라는 것은 그림에서 보면 두 벡터의 안쪽으로 볼 수도 있고 바깥쪽으로 볼 수도 있지요. 어느 벡터를 출발점으로 하느냐에 따라 다르게 볼 수 있습니다.)

김현승 님이 쓰신 글 :
: 안녕하세요
:
: 크리스 마스 연휴 잘 보내고 있나요???
:
: 질문하나 드립니다.
:
: 3군데 좌표가 있습니다.
:
: 1 : X: 100 Y: 100
: 2 : X: 50 Y: 150
: 3 : X: 100 Y: 200
:
: 이렇게 3 좌표에 대해서 각도를 계산하면 어떻게 하나요??
:
: 이럴 줄 알았다면 학교다닐때 삼각함수를 좀 공부할걸 그랬네요~~ㅠ.ㅠ
:
: 답변 좀 부탁드립니다.
:
: 감사합니다.